[Machine Learning] Naive Bayes Algorithm
in DeepLearning on Tech, Machinelearning
조건부 확률과 베이즈 정리
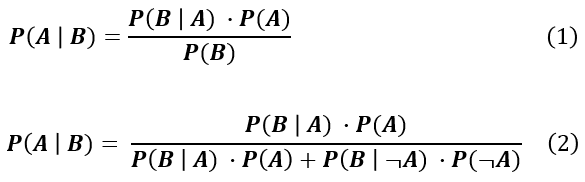
조건부 확률은 위식을 보면 알 수 있듯이 P(A|B)라 표기 하였을 때 이것의 의미는 B가 일어 났을때, A가 일어난 확률을 의미한다. 이러한 수학적인 이해는 예시를 즉 사례를 만들어서 확인하는 것이 좋다.
어떠한 병이 걸릴 확률이 0.1 %라 가정하자 이 병을 진단하는 장치는 병이 걸린 사람에게 99% 확률로 양성 반응을 보이고 암이 걸리지 않은 사람에게 1%확률로 양성 반응을 보인다고 알려져있다. 만일 내가 이 장치를 이용해 양성 여부를 테스트해보았더니 양성이라 나온 것이다. 이렇게 양성반응을 받았을 떄 실제로 암에 걸렸을 확률은 얼마나 될까?
위 사례에서 암이 걸리는 것을 H(hypothesis), 양성반응이 나온 것을 E(event)라고 부르겠다 이 때 구하려는 확률은 좌변과 같고 이는 베이지안 정리를 이용하여 우변과 같이 쓸 수 있다.
하지만 우변의 분모는 양성 반응이 나올 확률이고 이는 문제를 통해 알 수 가 없다 그러나 마찬가지로 조건부 확률을 이용하면 이를 다시 쓸 수 있다.
왜냐하면 양성이 나올 확률은 병에 걸리고 제대로 양성반응이라 할 확률 + 병에 걸리지 않았는데 양성이나올 확률이기 때문이다.
| 따라서 우리가 구하고자 하는 P(H | E)는 문제에서 제시된 내용으로 구할 수 있게 되고 이는 다음과 같다 |
이를 계산하면 9%가 나오게된다 이러한 베이즈 정리는 이미 알고 있는 확률들을 이용해 원하고자 하는 값을 얻을 수 있다는 큰 장점을 가지고 있다 하지만 베이즈 통계의 장점은 여기서 끝나지 않는데 바로 ‘학습’의 과정이 일어난다는 것이다 위의 예시를 조금더 연장시켜보자.
병에 걸렸을 확률이 9%라고 해도 다시 한번 장치를 이용해 암에 걸렸는지 테스트를 해보고자 한다 이때 다시한번 양성 반응이 나온 경우 병에 걸렸을 확률은 어떻게 될까??
이전의 식이 병에 걸릴 확률이 0.01%에 불과 하였던 것에 비하여 방금전 식을 통해 이번에는 병에 걸렸을 확률이 무려 9%나 상승 하였다. 이는 확률에 변화를 가져오게 되고 이번에 병에 걸렸을 확률은 무려 91%에 다른다.
따라서 사전확률로 대표되는 p(H)가 업데이트 되었고 , 이제는 이 값을 이용해서 내가 병에 걸렸을 확률을 구해야 한다. 베이즈 통게의 핵심은 데이터와 evidence가 많아지면 많아질 수록 우리의 지식이 ‘업데이트’되고 ‘향상’되는 데에 있다.
베이즈 정리와 머신러닝
그렇다면 베이즈 정리와 머신 러닝은 어떠한 문맥에서 공통점을 공유할 수 있을까? 머신 러닝을 대분류로 분류해보면 크게 regression과 classification으로 나타낼 수 있다. 먼저 회귀 문제를 살펴보면 독립 변수와 종속변수의 관게에 대해 추론하는 것이라고 할 수 있다.
예를 들어
이러한 식을 통해 만든 추정치 y’ 와 실제 y의 차이를 최소화 하는 것이 회귀의 목표이다 머신러닝은 선형회귀와 같은 알고리즘을 통해 ‘점진적으로’ 학습하여 parameter를 찾아간다 그런데 조금 시선을 바꿔서 우리가 추정하고자 하는 theta와 theta1이 하나의 특정한 값을 갖는 것이 아니라 분포를 갖는다고 생각해보자 그렇게 하면 우리는 머신러닝이 parameter를 찾는 과정을 베이즈 정리를 이용해 표현할 수 있게 되는데 다음과 같다.
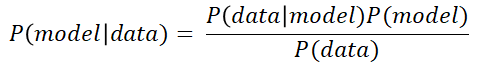즉 우리는 P(model)이라는 prior를 알 소 있는데 새로운 data가 관측이 되면 posterior(p(model|data))를 얻고 이를 다음번 학습의 prior로 사용하면서 점진적으로 p(model)즉 parameter들의 분포를 찾아가는 과정이 머신러닝 과정인 것이다.