선형대수를 수강하며 몇번이고 독학한 것이 기억이 나지 않는 경험을 하였다 이는 개념이 부족해서 그런 것이겠지..? 물론 머리가 나빠서 그런 것도 있겠지만 선형대수를 공부하면서 중요한 개념이나 코드를 정리하면 좋겠다해서 카테고리를 생성한다 또한 수학적인 이론을 세세히 파고 드는 것 보다 이해를 목적으로 하기에 어려운 내용은 거의 생략할 것이다… 공학도로써 수학을 이해하면 좋겠지만 느낌만 알면된다고 생각하기에 서론은 여기까지로 오늘 다룰 주제는 행렬곱이다.

---

행렬곱

Ax = b 라는 식을 보면 어떤 것이 떠오르는가? 본인은 이전에 독학을 하면서 A는 선형변환이라고 세뇌가 되었기에 x벡터를 b벡터의 선형변환이라 이해한다 하지만 기하학적으로 보게되면 A라는 공간에 x벡터를 투영한 벡터를 b벡터라고 볼 수 도 있다. 또한 대수적으로 보게되면 연립방정식으로도 볼 수 있다.

행렬곱은 일반적으로 다음과 같이 진행된다.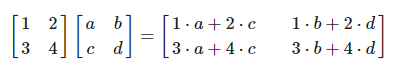

이는 왼쪽의 있는 행렬에서 행 하나를 가져오고 오른쪽에 있는 행렬에서 열 하나를 가져와서 계산하게 된다는 것을 알 수 있다. 가져온 행 혹은 열을 벡터로 생각한다면 계산된 행렬의 각 원소값은 벡터의 내적을 표현한 것임을 알 수 있다.

열벡터의 선형 결합

또다른 방식으로 행렬의 곱을 이해하는 방법은 열벡터의 선형결합으로 이해하는 방식이다 이번에는 행렬과 벡터의 곱에 대해 생각해보자

이때 다음과 같이 연산을 할 수 있음을 보인다 다시말해 행렬과 벡터의 곱은 행렬을 구성하고 있는 두 열벡터의 선형결합으로 다른 방식으로 표현 가능하다.

열공간을 기반한 해석

벡터의 선형결합 부분에서 설명했던 것처럼 벡터의 선형결합이 의미하는 것은 벡터공간의 생성이다. 즉 행렬과 벡터의 곱은 “주어진 열벡터를 통해 만들 수 있는 벡터 공간”을 말해 주는 것이다. 예를 들어 아래와 같은 문제를 보자

이 문제의 해답은 연립방정식으로 풀 수 있다.

하지만 아래와 같이도 생각 할 수 있다.

위 식을 처음 말했던 공간과 연관지어 생각하면 “두벡터 [1,3] 과 [2,4] 로 부터 생성된 벡터 공간 내에 [5,3]가 존재하는가? 만약 그렇다면 [1,3]과 [2,4]를 어떻게 조합해야 [3,5]를 구할 수 있을까? “ 이러한 관점을 이용한 선형대수학에서의 응용은 선형 연립방정식풀이와 선형 회귀가 있다.

선형변환을 기반한 해석

이 뿐 아니라, 행렬과 벡터의 곱이 열벡터의 선형결합이라는 해석이 우리에게 주는 또 다른 관점은 행렬과 벡터의 곱을 기저 벡터의 변형을 통한 벡터의 선형변환으로 해석 할 수 있도록 도움을 주기 떄문이다. 개인적으로는 이 해석이 제일 와닿는다.

예를 들어 행렬 를 이용하해 벡터

를 변환시켜보면

임을 아 수 있는데 이값은 새로운 두 기저벡터의 1배와 1배의 합으로 표현 될 수 있다.

(모든 내용은 공돌이의 수학정리 노트에서 공부한걸 그대로 정리한 것이다.)

이러한 관점을 이용한 선형대수학의 응용은 고윳값과 고유벡터, 주성분 분석(PCA). 특이값 분해(SVD)등이 있다.