행렬은 선형변환이다

임의의 벡터 a와 b 그리고 스칼라 c에 대해서 변환 T가 다음의 두 조건을 만족한다면 이 변화 T는 선형변환이다.

따라서 임의의 벡터 x,y에 대해 다음과 같이 성립한다.

여기서 집중할 부분은 원래의 기저벡터 두개를 아래와 같이 i_hat , j_hat이라 하고.새로운 기저벡터를 i_hat_new , j_hat_new라고 하자

T가 선형변환이라면 벡터[x,y]는 선형 변환 후에 새로운 기저벡터의 x배와 y배의 합으로 표현되어야 한다는 것이다.

예륻 들어, 행렬

를 이용해 벡터 변환 시키면 다음과 같다.

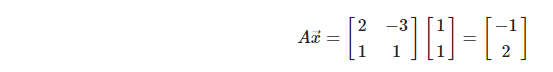
즉 아래와 같은 변화이다 선형벡터를 정의하는 기저벡터가 변함에 따라 기저벡터가 정의하는 공간안에 있던 벡터 또한 변하게 된다.

이를 보면 선형 변환의 결과로서 빨간점은 원래 기저벡터의 -1,2배로 표현되었지만 선형변환 이후의 새로운 기저벡터에 대해서는 1,1배로 표현된다.

permutation

기저벡터의 방향이 서로 뒤바뀌었다

projection on vector[1 2]

이와 같이 공간정보를 잃어버리는 경우도 있는데 이경우가 rank가 줄어드는 방향으로 선형변환이 이루어지는 예시이다