LU 분해

삼각행렬

lu분해를 이해하기 위해서는 삼각행렬에 대한 이해가 필요하다 아래그림을 보자

위 그림은 대각성분의 윗쪽 항들이 모두 0인 행렬이다 이러한 행렬을 하삼각행렬(lower triangular matrix)라고 하고, 아래와 같이 대각 성분 아랫쪽 항들이 모두 0인 행렬을 상삼각행렬이라고 한다.

연립 방정식의 풀이 다시 생각해보기

기본 행 연산을 통해 해를 얻어주는 과정을 우리가 다시 잘 생각해보면 가장 아랫쪽에 있던 방정식에서는 가장 마지막 미지수에 대한 식만을 남기고, 그 위에 있는 방정식은 마지막 두개의 미지수만을 남기는 식으로 미지수를 소거해 나가면 가장 아래에 있는 식으로 부터 마지막 미지수에 대한 값을 얻고, 그 위에 있는 식에 대입하는 과정을 통해 그 다음 미지수에 대한 값을 얻고.. 결국 모든 미지수를 알아낼 수 있다. (물론 정칙행렬에 한해서)

아래와 같은 연산을 수행

아래와 같이 수행

그러면 아래에서부터 차근차근 해를 구해 모든 미지수를 알아 낼 수 있다. 이러한 과정을 sub stitution이라고 한다.

Back substitution을 행렬로 표현

이러한 과정을 행렬로 표기해보자

즉 방정식을 행렬로 표시하면 다음과 같다

을 상삼각행렬로 바꿔주면 다음과 같다.

이런식으로 변형한다면 back substitution을 수행하여 해를 수할 수 있다. 얻은 행렬형태인 [A|b]에서 b를 빼게 된다면 이는 A의 상삼각행렬이 될 것이다.

기본 행렬의 역행렬을 곱하기 : LU분해

기본행렬들의 역행렬은 아주 간단한 형태를 띄고 있는데 간단하게 아래와 같다.

가령 아래와 같은 Row multiplication 행렬과 그 역행렬 관계는 다음과 같다

또 아래와 같은 Row addtion을 수행해주는 기본 행렬과 그 역행렬 관계는 다음과 같다.

행의 순서를 바꿔주는 기능을 수행해주는 기본행렬과 그 역행렬 관계는 다음과 같다.

그러므로 그림 2에서 볼 수 있었던 계수 행렬을 상삼각행렬로 만들어주는 연산에 대해서 계수 행렬 A앞에 곱했던 기본행렬들의 역행렬을 순서대로 곱해주면 아래와 같이 행렬 A를 다시 써줄 수 있게 된다 -> E3 E2 E1 I = A

기본행렬의 역행렬들을 직접 계산해주고 행렬 곱을 통해 이들을 하나의 행렬로 합쳐주면 하삼각행렬로 합쳐질 수 있음을 알 수 있다.

즉 행렬 A를 하 삼각행렬과 상 삼각행렬의 곱으로 나눠줄 수 있다는 것을 알 수 있다.

치환 행렬의 이용 : PLU 분해

어떤 행렬은 행교환 해주지 않으면 LU분해가 바로 되지 않을 수도 있다. 앞서 소개한 LU분해의 예시에서는 사실 행교환 연산은 이용하지 않은 경우였다. 이번에는 행 교환 연산까지도 포함되는 LU분해를 생각해보자.

아래와 같은 행렬 A가있다 생각해보자

이런 행렬은 하삼각행렬 꼴의 기본행렬중 row addition이나 row scailing만을 이용해서는 최종 상삼각행렬이 될 수가 없다.

따라서 하삼각 행렬꼴을 만들기 위해서는 A의 행을 바꿔 놓고 시작해야한다

이번 예시에서는 먼저 1행과 3행을 치환한 뒤 LU분해를 생각해보자 따라서

이라는 행렬을 A에 곱해주면

가 된다.

r2 -> r2 - (1/2)r1 연산을 수행해주면

와 같이 되는 것을 알 수 있으며 이 결과는 상삼각행렬임을 알 수 있다.

따라서, 기본 행연산의 역행렬을 취ㅐ 다음과 같이 써줄 수 있음을 알 수 있다.

이와같이 분해하고자 하는 행렬 A의 행순서를 미리 바꿔놓고 LU분해를 수행하느 ㄴ경우에 PLU분해를 수행한다고 한다. 앞서 행 치환 행렬의 역행렬은 자기자신이므로 원래 계수 행렬 A는 다음과 같이 분해될 수있다.

LU분해의 이용

만약 A가 정방행렬이고 A = LU 처럼 같이 분해 가능하다고 하면 다음과 같이 생각해볼 수 있다.

에서 A = LU라고 쓸 수 있으므로

이때, 만약 이 식을 다음과 같이 괄호의 위치를 밖꿔서 생각해보면

Ux 역시 일종의 열벡터이므로 Ux = c라는 열벡터로 치환해준다.

그런데 L은 하삼각행렬이고 하삼각 행렬은 forward subsititution을 활용하면 solution을 수월하게 얻을 수 있다. 그 다음

라는 문제를 풀어주면 x에 대한 답을 얻을 수 있게 되는 것이다 이때는 backward substititution을 사용하면 해를 쉽게 얻을 수 있다.

예를들어 위에서 보앗던 행렬 A를 LU분해하면 다음과 같다.

Ax= b에서 b = [6,5,17] 였다고 하면 LUx = b는

위식을 Lc = b로 바꿔주고 게산

그렇다면 c1 = 6 , c2 = -7 , c3 = 12 인것을 알았느니 Ux = c라는 점을 가져와 back-substitution을 수행한다.

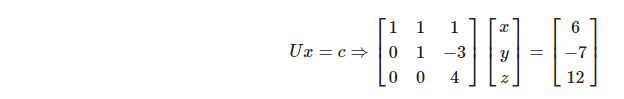
따라서 z =3 , y =2 , x=1임을 알 수 있다.