[Information Theory] Relation of Likelihood Estimation and SoftMAX and CorssEntropy

https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html 본 내용은 위 사이트에 친절하게 나와있으니 크로스엔트로피 개념이 기억나지 않는다면 방문하자

최대 우도 측정

우도란(가능성/가능도) - 나타난 결과에 따라 여러 가능한 가설들을 평가할 수 있는 측도(Measure)

최대우도 - 나타난 결과에 해당하는 각 가설마다 계산된 우도 값 중 가장 큰 값을 말함. 일어날 가능성(우도)이 가장 큰 것을 나타냄, 즉 관측된 랜덤표본에 해당하는 여러 가설중 우도 함수 값이 최대 인것

최대 우도 추정치(ML estimator)

-우도 함수 L(theata)를 최대로 하는 모수 theta값에 대한 추정치를 theta_라고 한다면 이는 우도함수를 미분한 값이 0이 되게 하으로 찾는다

-우도함수를 편 미분하여 0으로 두고, 미지의 모수인 추정치를 구하게 되는데 여기서 편 미분의 사용 이유는 우도 함수가 표본값 xI와 모수 theta에 모두 의존하기 때문이다.

최대 우도 추정법

위 그림처럼 결과값이 나타날 수 있는 최대한의 확률분포를 확률로 만들어낸다

-최대우도 원리란 나타난 결과는 여러 원인 중 일어날 가능성(조건부 확률)이 가장 큰 원인에서 비롯된다는 원리를 말한다.

-최대 우도 추정법은 우도함수를 최대화 하면서 모수를 추정하는 방법인데 관측된 표본에 기초하여 관측 불가능한 파라미터(모수)를 추정하는 방법론 중 하나이다 다시말해 표본들로부터 알려지지 않은 모집단 확률분포의 형태를 추정해가는 방법론이다.

-최대우도 측정법은 모집단이 어떤 종류의 확률 분포를 하는지 정도는 알고 있으나 구체적으로 모집단을 나타내는 수치를 모르는 경우에 주로 사용한다

최대우도 추정법 쉽게 이해하기

우도의 개념을 단순하게 정의하면 확률가 그 의미가 대칭되는 것과 같다. 다시 말해 확률에서는 모비율이 특정되어있고 불변인데 그 위에서 관찰된 값이 나오는 반면(동전을 던질 때 앞면이 나올 확률은 일반적으로 1/2이며 그것을 바탕으로 특정 관찰이 나올 확률을 계산한다) 우도의 개념에서는 역으로 관찰치는 고정되어있고 그것이 가장 잘 그럴 듯하게 나오는 모수 값을 찾아내는 것이다(확률분포를 찾아나감)

이를 2차원 그래프로 나타내면 확률 분포곡선에서 특정한 포인트를 찍어서 확률을 계산하는 확률과는 정반대로 우도의 개념에서는 특정한 관찰값이 이미 주어져있고 이에 끼워맞추어 그 관찰값이 제일 잘 나오는 확률분포곡선의 위치를 찾는 것이 그 목적이다. 이는 회귀문제와도 비슷하다고 볼 수 있는데 데이터셋을 설명하는데 있어 가장 그럴듯한 가설 h(x)를 찾는 과정과 비슷하다.

이는 일반적인 회귀분석이 갖고 있는 문제점과 한계점에 대응하기 위한 것이 일부이며 이것이 갖고 있는 최대의 문제점인 계산문제가 컴퓨터의 발전으로 해결되었기 떄문이다. 특정한 확률분포를 사용해 계산하여 우도를 구하고, 그 분포를 약간 이동시켜 또 우도를 구하고 반복하다가 그 우도가 최대로 결정되는 지점에서 멈추는 것이다

마지막으로 최대우도 추정의 가장 큰 장점 중 하나는 확률 분포의 종류만 정해지면 게산방식은 모두 동일하다는 것이다. 특히 일반적인 방식에서 각각 모두 다른 표준오차의 추정 역시 같은 방식으로 계산되며 표현될 수 있다는 것 이는 결국 확률분포만 확보해 표현할 수 있다면- 일반적인 routine으로 처리 할 수 있다는 과정을 시사한다, 아울러 최대우도 추정은 특정한 어떤 분포가 아니라 그런 방식을 사용하는 분석방법을 통칭하는 일종의 전략이라 생각하도록 하자

## Classfication문제에서 CrossEntropy를 사용하는 원리와 방법론

위 수식은 cross entropy의 일반식 아래식은 binary cross entropy의 식이다

Multi-Class Classfication

각 샘플은 클래스 C중 하나로 분류 될 수 있다. 해는 0번 [1,0,0] 달은 1번, [0 1 0],구름은 2번, [0 0 1]으로 분류될 수 있다는 것이다.

CNN은 s(scroe)벡터를 출력하고 one hot 벡터인 타겟벡터와 t와 매칭이 되어 loss값을 계산할 것이다 즉, Multi-Class Classification은 여러 샘플(이미지)에서 C개의 클래스 중 하나의 클래스로 분류하는 문제로 생각할 수 있다.

활성화 함수(Activation Function)

Sigmoid 와 softmax 함수가 있고 이 중 softmax함수는 클래스의 스코어를 나타내는 벡터 각각의 요소는 (0,1)이 되며, 모든 합이 1이 되도록 만들어 준다 s_j는 각 스코어이고 모든 i에대해 소프트 맥스 값을 더하면 1이 나온다.

Cross Entropy의 이해

https://theeluwin.postype.com/post/6080524 참고문헌

딥러닝과 머신러닝을 하다보면 크로스 엔트로피 함수가 많이 등장한다 정확하게는 분류문제를 풀 떄 크로스 엔트로피를 이용해 손실 함수(loss function)을 정의 하고는 한다. 아래는 크로스 엔트로피 함수이다

이식 그리고 엔트로피 자체에 대해서는 여러가지 관점으로 해석 가능하다 왜 엔트로피 관력 식에는 항상 확률의 로그가 등장하는가? 와 같은 애기들이다.

여기서는 어떠한 분포간의 “차이”(divergence)에 대해 집중을 한다. 머신러닝 /딥러닝은 대부분 정답 분포를 모사하는 것이 목표가 되고, 얼마나 근접했는지를 수치화 해서 피드백을 주는 방식으로 구성된다 보통 두 분포간의 차이를 정의할때는 KL-발산이라는 식을 주로 사용한다 KL발산은 다음과 같이 정의된다.

두 확률의 비율에다가 로그를 씌운것이다 이는 가짜 분포 q(x)가 진분포 p를 얼마나 잘 따라했는가에 대한 값을 타나낸다고 해석을 한다 “차이”느낌의 값이기 때문에 작을 수록 좋은 상황인 것이다 실제로 px = qx라면 위 값은 0이 된다. 다만 이 식이 담고 있는 함의를 느끼기엔 다소 어색한 부분이 있는데 잘 살펴보면, 확률 비율과 관련된 무언가의 기댓값이라고 생각 할 수 있다.

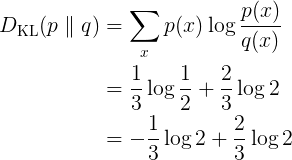
보변 qx가 px보다 클때 즉 넉넉하게 예상했을때는 패널티를 깍아준다 반면 qx가 px 보다 작은 상황 즉 부족하게 예상을 하면 패널티가 발생한다. 그리고 px 나 qx나 확률이기때문에 모든 x에대해서 합을 구하면 항상 1이기 떄문에 확룰을 적절하게 분배햐야하는 상황이되고 따라서 어딘가에서는 qx가 px보다 크고 또 어디선가는 작게된다 그리고 패널티의 가중치는 px로 주는 것이기때문에 부족하게 예상을 함에 대해 패널티를 주고 있는 것이다.

이 KL발산은 두 분포간의 차이를 나타내 주는데 그렇다고 거리가되지는 못한다. KL발산이 항상 0이라는 것은 대칭적이지 ㅇ낳기 떄문에 거리의 조건을 만족하지 못했다.

약간의 변형을 통해 KL발산과 엔트로피 , 그리고 크로스 엔트로피가 서로 싶은 관게에 있는 식들임을 알 수 있다 머신라닝/딥러닝의 원래 목표인 분포따라하기를 생각해보면 진분포 p가 있고 이를 우리의 확률 모델 q가 따라하도록 해야한다 즉 KL(P||Q)가 줄어들면 되는 딱 들어맞는 상황 인 것이다 그래서 이 KL가 작아지도록 경사하강법등을 사용해 파라미터를 학습한다.

그런데 분류 문제를 풀 때엔 보통 분류 문제를 딥러닝으로 풀려고 할 땐, 뭔가 인풋 a가 있고, 신경망이 마구 나오고, 마지막에 가서는 분류 해야 하는 클래스 수 만큼의 차원으로 보낸 뒤, 소프트맥스 함수를 취한다 소프트맥스의 역할은 C개의 실수값을 합이 1인 분포값들로 바꿔주는 것입니다. 즉, 가장 마지막 레이어의 결과값은 곧 이 인풋이 각 분류 클래스일 확률을 알려주는 것이다.

다시 말하자면, 일반적인 분류 신경망 모델의 가장 마지막에 있는 소프트맥스 레이어를 통과하면 보통 C개의 확률값들이 나오고, 이는 현 인풋이 각 분류 클래스일 확률을 나타내주는 일종의 분포가 된다. 여기서 확률값이 가장 높은 번호를 우리는 a의 클래스로 예측하는것이다