[CS231N] lecture3 review
in Summary on Summary, Cs231n
손실함수
이전에 KNN알고리즘은 그 한계가 명확하고 성능또한 보장하지 못하여 가중치를 학습하여 그럴싸한 가설을 만드는 방법을 통해 그 성능을 올렸다. 일단 가설을 f(x , W) = Wx의 1차 함수라 둔다면 이를 학습하는데 있어 보조적인 역할을 하는 것이 바로 손실함수이다 손실함수는 본 가설이 얼마나 정답레이블과 비슷한지를 정량화 하였다고 보면된다.
SVM

SVM loss 는 가설 (= 모델이라 하겠다) 모델이 각 카테고리에 대해서 예측한 점수와 실제 레이블과의 점수비교를 통해 함수를 정의한다 s_j 는 모델 에측값이며 s_i는 실제 레이블이다. 이때 추가적으로 +1을 해주게 되는데 이는 여유공간을 둠으로써 수치상 애매한 값들을 지우고 확실하게 차이 나게 하기위해 더해준 값이다. 이러한 SVM알고리즘은 함수의 형태가 힌지와 닮아 힌지함수라 부르기도 한다.

실제로 예시를 들어 설명한다면 위 그림과 같이 실제 손실값이 2.9로 나온다. 위와 같은 방식으로 차에 대해서 적용하면 차에 대해서는 모델이 예측을 잘했기때문에 손실값이 0이 나오게된다. 이렇게 구한 3가지 loss를 더한다음 평균을 취해준것이 SVM 손실함수의 값이다.
추가개념
추가적으로 강의해서는 몇개의 질문에 대한 답을 하게된다.
- what is the min/max possible loss?
모든 예제에있어 모델이 올바르게 예측을 한다면 loss값은 0이 될것이며 힌지함수의 형태를 통해 손실값은 무한으로 발산한다는 것을 알 수 이싿,
- At initalization W is small so alls ~ 0. What is the loss?
score값이 0에 수렴하게된다면 1을 넘지 못하므로 손실값또한 0으로 고정되게 된다.
추가적으로 우리가 L =0이되는 가중치를 찾았을때 이러한 가중치가 유니크하냐는 질문에 2W또한 L=0이 되므로 그렇지 않다고 할 수 있다.
Regularization

데이터를 학습하는 과정에서 모델이 training data에만 맞게 학습되어 실제로 성능을 평가하는 test data 에서는 잔혀 다른 값을 예측하는 상황을 overfitting이라고 한다 이러한 오버피팅은 모델을 단순하게 만들어줌(규제) 함으로써 해결가능한다 위 그림의 식과 같이 손실함수에 regularization항을 더해줌으로써 해결가능하다. 이러한 정규화항은 가중치의 영향력을 약하게 만들어 준다 따라서 모델은 더 유연한 형태를 만들 수 있게 된다.

정규화항은 위와 같은 항들이 존재한다. 정규화 식은 최종적으로 W의 값을 줄이기 위해 넣어준다.
Softmax Classifierd

소프트 맥스함수는 이전에 정리한 포스트를 통해 공부를 하였다 이는 sigmoid함수와 같은 활성화 함수중 하나로 그 특징은 카테고리별 score에 exp를 해주고 normalize를 해줌으로써 각 점수를 확률로 나타낼 수 있게 된다 이는 이후 우도 손실과 크로스 엔트로피 손실함수와 관련이 있게 된다.
위 그림은 sofmax함수의 예시인데 보시다싶이 wx+b를 통해 산출된 카테고리별 점수는 우도손실함수를 통해 손실함수를 얻어낸다
Recap
즉 지금까지 과정을 살펴보면 아래와 같다.

optimizer
손실함수를 구했다면 어떻게 손실함수의 최솟값을 얻어 낼 수 있을까 몇몇의 방법을 optimzier라 말하며 optimizer중 하나는 gradient descent이다. gradient descent는 하나의 협곡에서 최저점을 찾기 위한 방법이라 생각하면 쉽다 최저점을 찾기 위해서는 어떤 방향으로 얼마만큼 내려가는 것이 중요한 요소로 작동하는데 어느 방향으로 갈지는 특징들의 편미분을 통해 경사하강법을 수행하여 얻어 낼수 있으며 얼마만큼 갈지는 하이퍼파라미터를 임의로 설정함으로써 정의가능하다.
미분을 하는 방법은 두가지로 나뉘게 되는데 하나는 수치미분이며 다른 하나는 해석미분이다 머신러닝에서는 항상 해석미분을 사용한다 하지만 수치미분을 통해 확인 작업을 하는데 이를 gradient check라고 말한다.

위 그림은 하이퍼파라미터중 stepsize에 따른 학습률을 나타낸다 이를 통해 stepsize는 너무 커서도 안되며 너무 작아도 안된다는 것을 보여준다 따라서 좋은 step size를 찾기위해 휴리스틱한 방법으로 노력해야만 한다,.
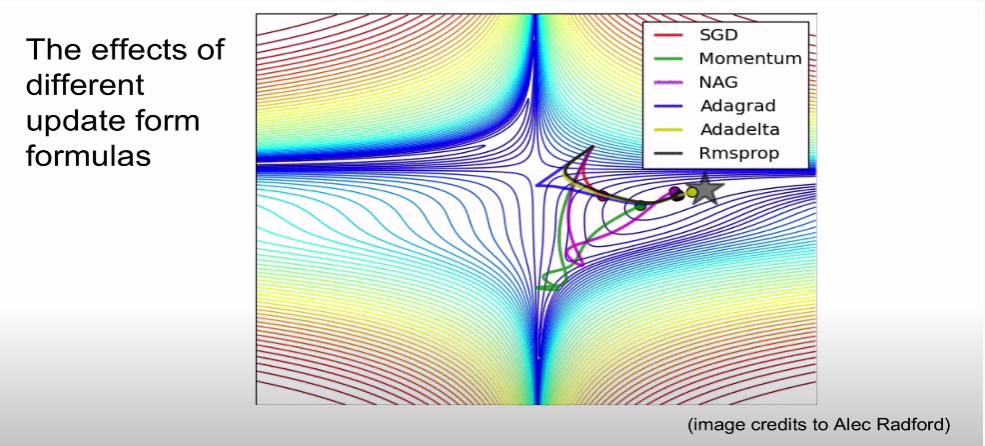
optimizer에는 여러 방법들이 있다 위 그림은 경사하강법의 응용버전들이 있는데 최근에는 성능이 제일 잘 나오는 rmsprop를 사용한다.