[CS231N] lecture7 review

Training Nerual Networks Part2

이전강의 preview

하이퍼 파라미터의 최적값을 서치하는 방법론에 대해서도 언급한다 넓은 범위에서 시작하고 싶을 때 쓰면 좋다. 몇 번씩 반복하면서 하이퍼 파라미터의 범위를 좁히는 방법을 사용한다 파라미터들마다 각각의 sensitivity가 다르다 예를들어 learning rate는 굉장히 sensitive하지만 regularization은 그렇지 않다

optimization

SGD

optimization의 목표는 최소의 loss값을 갖는 w를 찾는 것이다 SGD는 매우 간단하지만 문제를 갖는다 위 그림 처럼 W1 ,W1인 2차원으로 생각 할때 빨간점에서 최적점으로 갈 때 수평으로 이동하면 매우 느리고 수직으로 이동하면 비교적 빠르다 LOSS가 수직 방향으로만 SENSITIVE해서 동일하게 이동하지 못하고 지그재그로 이동하게 되는 것이다 high demension일 수록 더욱 문제가 심각해져서 큰 문제이다.

또한 파라미터w와 loss function의 관계함수가 구불구불해서 기울기가 0이 되는 지점이 극소값이 아닌 경우의 문제이다 이는 위처럼 2개의 문제로 분류가 된다.

1.local minima

슬라이드 중 위에 있는 사진의 경우입니다. 극대값들 사이의 극소값(기울기가 0이 되는 지점)에 안착하게 되는 경우이다.

saddle point 슬라이드의 아래있는 사진의 경우입니다. 얘는 local minima 보다 더욱 골치 아픈 문제가 되는데 데이터가 더욱 고차원일수록 잘 일어나고, 기울기 0의 주변 지점의 기울기가 매우 작아져서 update도 굉장히 느려지는 문제가 발생합니다.

마지막 3번째 문제점은 SGD의 S인 Stochastic이 문제를 일으킨다고 한다 미니 배치를 쓰는 SGD알고리즘은 미니배치마다 loss를 계산하여 전진해나가는데 이는 강의에서 expensive라고 하는데 비료율적이라는 의미이다

SGD + Momentum

어느 한 점에서 특정 포인트를 찾는 과정을 물리적인 관점으로 볼 수 있다. 이는 운동량을 개입하는 시키는 것인데 위의 vx코드를 보면 rho*vx로 step이 이루어져서 기울기가 0인 지점에서도 update가 되는 알고리즘이다.

여기서 v는 가속도를 의미하며 rho는 보통 0.9 , 0.99를 이용하여 가속도에 약간의 마찰값을 넣어주는 파라미터이다. 매 step에서 old velocity에 friction으로 감소시키고 현재의 gradient를 더해준다.

슬라이드 공은 기울기가 0인 지점에서도 가속도로 step하기 때문에 update가 진행된다 또 하나의 장점은 tacoshell의 문제를 어느정도 해결해줍니다.

기존 SGD는 지그재그로 최적화가 되어 poor conditioning이지만, 모멘텀 + SGD는 모멘텀이 수평방향으로는 가속도를 유지하여 민감한 방향으로의 총합을 줄여주는데 gradient의 추정값들에서의 noise들을 평균화 시켜주는 역할을한다.

Nesterov Momentum

쪽 그림을 먼저 보면, 실제로 이 두 벡터 방향의 average로 업데이트를 하는데 이게 바로 gradient의 추정값의 noise를 줄여주는 것이다. 오른쪽 장면에서 빨간 스타트점에서 velocity방향으로 출발한 뒤 거기서 gradident를 게산한다. 그리고 다시 원점에서 actual step으로 최적화를 진행한다. 계산 순서의 차이가 있는데, Convex optimization에서는 잘 작동하지만, Neural Network와 같은 non-convex의 문제에서는 보장된 방식은 아니다.

위 수식을 보면 파란색 네모칸의 식이 달라졌는데 미리 속도 즉 velocity 방량을 에측해서 gradient를 구해준다는 의미이다

AdaGrad

위 방법은 각각의 매개변수에 맞춤으로 갱신을 해주는 알고리즘이다 훈련도중 계산되는 gradient를 활용하는 방식으로 velocity 대신에 grad squared term을 사용한다 학습도중에 계산되는 gradient에 제곱을 해서 계속 더해준다

그러므로 분모의 값이 점점 커지므로 step이 진행될 수록 값이 작아진다. 다시 말해 처음에 올바른 지점으로 접근 할때 속도가 빨랐다가 점차 속도가 느려진다는 것이다 convex할때는 minimum에 서서히 속도를 줄여서 수렴하면 좋다 하지만 non convex할때는 saddle point에 걸려 멈출 수도 있기에 문제가 된다 이러한 문제점의 해결책으로 RMSProp가 나온다.

RMSProp

RMSProp은 AdaGrad의 gradient 제곱항을 그대로 사용한다. 하지만 이 값들을 누적만 시키는게 아니라 파란색 상자와 같이 decay_rate를 곱해준다 보통 decay_rate는 보통 0.9 또는 0.99를 사용한다. 그리고 현재 gradient 제곱은 (1-decay_rate)를 곱해주고 더해준다. 이는 adagrad와 매우 비슷하기에 step의 속도를 가속/감속하는 것이 가능하다. 이를 통해 속도가 줄어드는 문제를 해결하였다.

Adam

위에서 본 모멘텀과 adagrad를 잘 합쳐서 활용한 알고리즘이 바로 Adam이다 아담은 first moment와 second moment를 이용해서 이전의 정보를 유지시킨다. 빨간색 상자(first)는 gradient의 가중합이다. 파란색 상자(second)는 AdaGrad나 RMSProp 처럼 gradients의 제곱을 이용하는 방법이다. 마치 모멘텀과 RMSProp을 합친 것과 같이 보인다. 근데 초기 step에서 문제가 발생한다고 한다.

식을 보면 first_moment와 second_moment가 0이다. 근데 second_moment를 1회 update하고 났을 때 beta2는 decay_rate이니까 0.9 또는 0.99로 1에 가까운 수이다. 그렇기 때문에 1회 update 이후에 second moment는 여전히 0에 가깝다. 이후 update step에서 second_moment로 나누게 되는데 나눠주는 값이 작다보니까 분자가 커져서 값이 튈 수도 있다고 한다. 값이 크면 step이 커져서 이상한 곳으로 튀어버릴 수도 있다.

그래서 이를 해결하기 위해 보정항을 추가한다. (1e-7는 나누는 값이 0이 되는 것을 방지한다.) first / second moment를 update하고 현재 step에 맞는 적절한 bias를 넣어줘서 값이 튀지 않게 방지하는 것이다.

find learning rate

위에서 본 방법 모두 learning rate를 가지고 있는데 이를 구하기 위해서는 다양한 방법이이 있다 물론 쉽다고 하지는 않는다 decay learning rate같은 경우 처음에 leaning rate를 높게 설정하고 학습이 진행될 수록 점점 낮추는 것이다.

위 내용은 ResNet논문에서 나온 내용이다 step decay leearning rate전략을 이용해서 loss를 나타낸 것이다 평평해지다가 내려가는 구간은 learning rate를 낮추는 구간이다

Beyond Training Error

우리는 loss를 줄이면서 train과 val의 격차를 줄여야만한다 이 간격이 넓어질수록 오버피팅된다는 것인데 이를 위해서 몇가지 방법을 소개한다.

Model Ensembles

다른 방법으로 모델을 독립적으로 학습시키는게 아니라 학습 도중 중간 모델들을 저장(snapshot)하고 앙상블로 사용할 수 있다고 한다. 그리고 test때에는 여러 snapshots에서 나온 예측값들을 평균을 내서 사용한다.

여기서 스냅샷은 구간을 정해놓은 지점이다. 훈련을 하는데 10개의 체크포인트를 두어서 10번째마다 새로 하겠다라는 식의 구간이라고 생각하면 된다. 이게 앙상블을 사용하면 모델을 여러 개 만들기 때문에 그만큼 시간 소모가 든다. 그 방법 대신에 한 모델 안에서 10개의 구간을 두고 마치 앙상블처럼 하겠다는 것이다.

위의 슬라이드에서 빨간색을 보면 train loss가 낮아졌다가 갑자기 올라가고 그러는데

이게 어느 지점에서 learning rate를 엄청 낮췄다가 높였다가를 반복하여

손실함수가 다양한 지역에 수렴할 수 있도록 하는 것이다.

이러한 앙상블 기법으로 모델을 한번만 train 시켜도 좋은 성능을 얻을 수 있다고 한다.

Regularization

하지만 앙상블 기법은 모델을 여러개 만들기 떄문에 효율적이지 않다. regularization은 모델이 학습마다 다른 모델을 학습하게 만들어 training data에 fit하게 만들지 않는다.

이전에 배운 L1 , L2 규제항은 뉴런네트워크에서 잘 작동하지 않는다고 한다 따라서 나온것이 dropout이다.

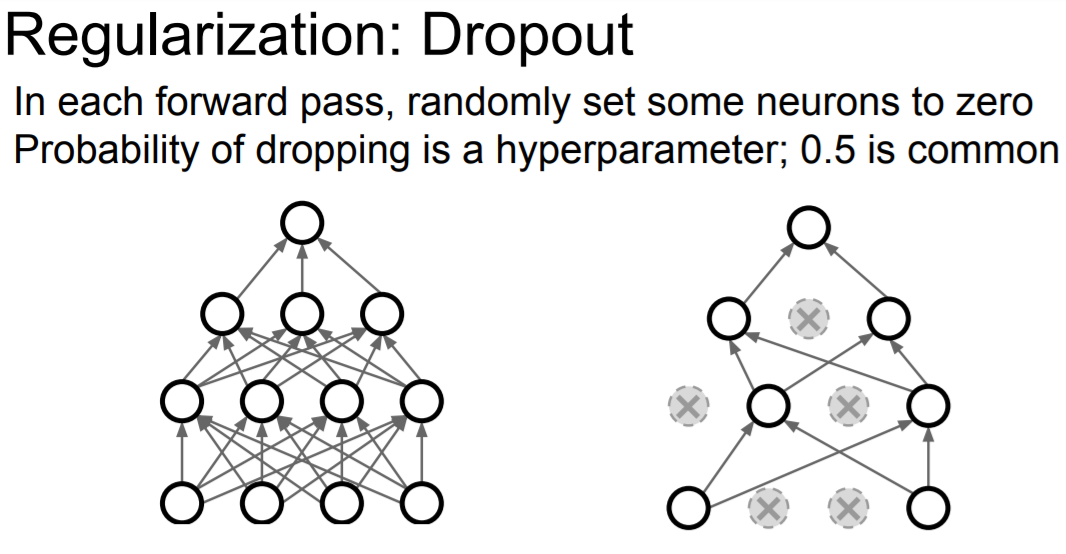forward pass 과정에서 일부 뉴런을 0으로 만드는 것이다.

오로지 뉴런의 일부만 사용하고 있다. forward pass 반복마다 그 모양은 계속 바뀐다. 현재의 activatons의 일부를 0으로 만들어 다음 레이어의 일부가 0과 곱해지게 하는 것이다.

특징은 feature들 간의 상호작용을 방지하는 것이다이후에 모델이 고양이라고 예측할 때 다양한 features를 골고루 이용할 수 있도록 한다.

따라서 dropout이 오버피팅을 어느정도 막아준다.

단일 모델로 앙상블 효과를 가질 수 있다.

dropout은 아주 거대한 앙상블 모델을 동시에 학습시키는 것과 같다.

즉, forward pass마다 dropout을 랜덤하게 하니까

forward pass마다 마치 다른 모델을 만드는 것처럼 효과가 나오게 될 수 있다.

dropout = 0.5로 학습시킨다고 생각해보자. 4가지의 경우의 수가 존재하고, 그 값들을 4개의 마스크에 대해 평균화 시켜준다. 이 부분에서 train/test 간 기대값이 서로 상이하다. test가 train의 절반밖에 되지 않는다. 이를 해결하기 위해 dropout probability를 네트워크의 출력에 곱한다. 그렇다면 이제 기대값이 같아졌다. 일부노드를 무작위로 0으로 만들어주고 test time에서는 그저 값 하나만 곱해주면 된다.

하지만 우리는 test time이 매우 작았으면 하기에 train time에 작업을 해주어 이를 해결한다 위그림에서 처럼 test에 p를 곱하던 것을 train time에 p를 나누어준다.

정리하자면 train time에서는 네트워크에 무작위성을 추가해 training data에 너무 fit하지 않게 한다. test time에는 randiomness를 평균화 시켜서 genneralization효과를 주는 것이다 BN도 비슷한 역할을 할 수 있다. 그래서 BN을 할때 dropout을 사용하지않는다(사용하지 않는사람도 있고 그렇지 않다는 사람도 있다)

etc

그외에도 data augumentation을 통해 데이터의 종류를 늘려 학습을 원할하게 하거나 모델의 일부를 변형하여거나 없애 다양한 모델에서의 학습을 의도한다 이러한 기법들의 공통점으로는 학습과정에서 random을 주어 다양한 조건속에서 학습하게 유도하고 test과정에서 이를 일반화 시키는 것이다.

Transfer Learing

원하는 양보다 더 적은 데이터만을 가지고 있을 때 사용하는 방법이다.

가장 마지막 FC layer는 최종 feature와 class score간의 연결인데 이를 초기화시킨다. 그리고 차원을(ex. 클래스 수만큼으로) 줄이고, 마지막 레이어만 가지고 우리 데이터를 학습시킨다.

데이터가 조금 많다고 생각되면 전체를 fine tuning 해볼 수도 있다.

다음과 같이 경우에 따라 적용시키면 매우 효율적인 결과를 얻어낼 수 있을 것이다.