[CS231N] lecture12 review

Generator Model

generator 모델은 이미 gan을 통해 고화질 이미지를 생성할 수 있게 되었고 이전에 나온 논문중에서는 알면 좋은 점들만을 가지고 요악할 것이다

또한 gan은 assginment를 통해 더 알아 볼 예정이다.

Autoe Encoder

auto encoder는 데이터 생성 모델이 아닌 학습 데이터에 대해 보다 낮은 차원의 feature representation을 학습하는 것이 목적이다 구조는 다음과 같다.

즉 input data x 그 자체를 label로 삼아 저차원의 feature z를 학습하겠다는 것이다 학습에 쓰이는 encoder와 decoder로는 linear + ninlinearlity(sigmoid) fullyconnected , ReLU CNN등이 사용된다

Variational AutoEncoder(VAE)

이는 autoencodr를 generative Model로 사용하기 위해 sampling과 확률적 개념을 집어 넣은 것이다.

생성모델을 만든다는 것은 training data set x의 분포로부터 임의로 샘플링한 이미지를 생성하는 모델을 만든다는 것이다. 따라서 주어진 데이터x의 분포 p(X)를 구해야한다. 사람들은 P(x)의 수식 자체를 직접 정의하기 보다는, 어떤 latent variable z의 기댓값으로 x를 표현하는 방법에 대해 생각하게 된다. 이미지의 요약본 z를 통해 이미지 x를 복원하 룻 있으므로 training data x의 분포 p(x)또한 x와z의 joint distribution p(x,z)가 있을 때 이를 z에 대하여 적분한 x의 marginal distrubution으로 표현 가능하다고 한다(나도 정확히는 모르겠지만 식을 보니 조건부확률의 적분합으로 보아 대충 이해를 한다)

문제는 계산이 되지 않는다는 것인데 먼저 P(z)의 경우, latent variable의 prior distribution이다. 여기서 일반적으로 prior distribution을 gaussian distribution으로 가정한다. 생각해 보면, 사람 얼굴 이미지를 생성할 때 z에는 웃음의 정도, 눈썹 위치 등이 있을 수 있다. 일반적으로 이러한 특징들은 정규분포를 따르므로 합리적인 생각이다. (추후에 GAN에서는 prior distribution을 직접 input으로 학습시킨다. VAE의 단점이 이러한 가정에서 나온다고 할 수 있음)

그럼 계산이 안되는 이유는?? P(x

z) 때문인데, 모든 z에 대해서 P(x

z)를 계산할 수 없기 때문이다. Bayes 정리를 이용하여 P(z

x)로 순서를 변환해도 계산이 불가능 한 것은 마찬가지인데, 아래 수식에서와 같이 P(x)를 구할 수 없기 때문이다. (구하고자 하는 것이 P(x)이므로)

VAE의 최종 구조 및 lower bound를 통한 intractableness해소

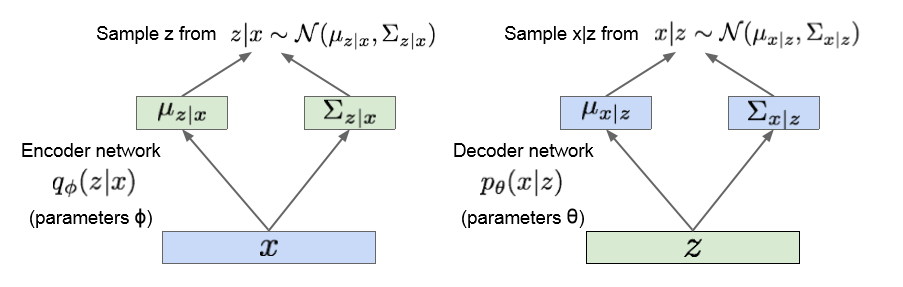
그림은 먼저 x를 input으로 Encoder network를 학습하여 P(z	x)의 분포를 찾아 내겠다는 의미이다. 찾은 부포에서 z를 몇개 sampling 하여 decoder network에 대입
하고 이로부터 p(x	z) 이떄 필요한건 가우스 분포를 따른다고 가정했으므로 평균과 공분산이 필요하다.

궁극적으로 VAE를 학습시키는 방향은 p(X)를 최대화 하는 방향이다 p(x)보다는 log p(X)가 최적화 하기 쉬우므로 log를 쓰워 주고 이를 앞서 정의한대로 z에대한 기댓값으로 표현해 보면 다음과 같다.

phi(Φ)는 무엇인가 불편한 마음이 들 텐데, Encoder neural network의 가중치 행렬, 즉 parameter를 의미하는 것이다. 즉 Encoder network에서 update시켜야 할 대상은 Φ가 된다.

이를 풀면 위와 같다는데… 여기서 VAE의 한계점이 드러나는데 바로 맨 아래수식 또한 정확하게 계산할 수 없다는 것이다. 때문에 lower bound르 ㄹ구하고 이를 최대화 함으로써 목적식을 최대화 하는 것에 가까워지고자한다.

계산을 할 수 없느 이유는 말하면 우선 첫 번쨰항은 decoder entwork의 출력인 p(x|z)이므로 얼마나 inpt data가 잘 reconstruct되었는지를 의미한다 이것은 계산가능하다 두 번째항은 KL-divernce인데 q(z|x)와 p(z)사이의 유사도를 의미한다 q(z|x)는 공분산 행렬을 가정한 가우시안 p(Z)역시 가우시안이므로 이 값을 구할 수 있다.

마지막 항이 계산 불가능한 항이다 맨 처음 정의한 적분 식에서와 같이 p(z	x)느여전히 구할수 없다 하지만 이는 거리이므로 항상 0보다 크거나 같다
따라서 마지막 항을 제외한 나머지 수식을 lowerbound로 지정하고 최적화해준다. 다시 lowerbound를 살펴보면 첫번째 항은 p(x	z)항이므로 input data가
잘 복원 될 수록 그 값이 커진다 두번쨰 항은 q(z	x)와 p(Z)의 KL term이므로 0에 가까울 수록 두 분포가 가까워지게 된다

따라서 이게 전체적인 과정이다 먼저 x가 encoder를 통과하여 q(z|x)를 구한다 q(z|X)로부터 z샘플링을 하여 이를 decoder에 대입하여 p(x|z)를 얻는다 이후 objective function값을 구하고 이르 ㄹ기반으로 back-propagation encode:psi를 update decodertheta를 업데이트

위그림은 VAE로 이미지를 생성한 결과이다 즉 최종적으로 학습시킨 decoder의 p(x

z)분포에서 샘플링한 이미지가 되겠다. 임의로 특징 z1과 z2를 정하고, 두 가지를 축으로 값을 조금씩 변화하며 이미지를 샘플링 한 결과이다.

이미지가 자연스럽게 연속적으로 변화하는 것을 볼 수 있다.